艾伯|比费马大定理还难的数，数学家证明1不是同余数，花了一千多年！史密斯

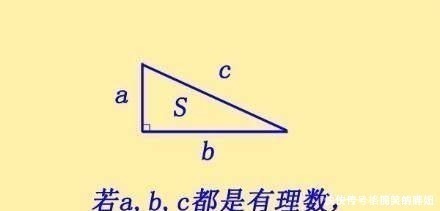
数学中有各种数，比如奇数，偶数，素数，完美数等等。其中有一类数，性质非常难掌握，叫做同余数。定义：若直角三角形的三条边都是有理数，那么这个三角形的面积，叫做同余数。

文章插图

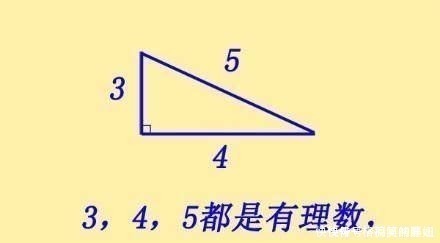
其中，人们只对那些，是整数的同余数感兴趣，叫做同余整数。比如3、4、5组成的直角三角形，面积为1/2×3×4=6，那么6就是同余数。最小的同余整数是5，对应最小的直角三角形，边长分别为：3/2，20/3，41/6。

文章插图

最早提出同余数概念的是阿拉伯人，一千多年前，他们提出这样一个问题：一个正整数n，何时能存在一个有理数x，使得x-n，x和x n都是有理平方数？这就是同余数问题，其中n就是同余数。阿拉伯人还给出了30个特殊的同余数，其中包括：5，6，14，15，21，31……。

文章插图

那么问题来了，1是同余数吗？会存在一个直角三角形，其三边都是有理数，然后面积等1吗？阿拉伯人回答不了这个问题，还有2和3是否是同余数？也不知道。直到一千多年后的1659年，法国大数学家费马（就是因为空白太小，写不下费马大定理美妙证明的那个费马），他利用独创的无限下降法证明了1，2和3都不是同余数。

文章插图

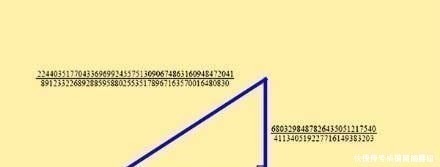
差不多100年后，大数学家欧拉证明了7是同余数。随着数值的增大，判断一个数是否是同余数，变得非常困难，甚至强大的计算机利用地毯式搜索也是不易的。比如157是同余数，对应的直角三角形最小解就非常复杂：

文章插图

同余数问题，是数学界的三大千年难题之一，比费马大定理和古希腊三大几何问题难多了。直到现在为止，同余数问题也没有得到彻底解决，同余数问题和某些特殊整数方程相关联，比如判断1是否是同余数，等价于费马大定理中n=4的情况。

【艾伯|比费马大定理还难的数，数学家证明1不是同余数，花了一千多年！】
文章插图

经过上千年的探索，数学家总结了无数经验，最终提出同余数中的一个重要猜想——BSD猜想（猜想涉及深奥的数学知识，所以此处不做描述），在2000年被列为七大千禧问题之一。对BSD猜想的研究，至今学术界没有任何公开的进展。好啦！这篇内容就和大家分享到这里，喜欢我们的读者朋友，记得点击关注我们——艾伯史密斯！